Banger Casino catches the eye thanks to its sleek design and impressive catalog of games. It accepts BDT and operates under a Curacao license. You can legally join it if you live in Bangladesh and are aged 18 years or older.
In this article, we’ll explain to you what’s so special about this casino brand. You’ll learn about the available entertainment options, deposits and withdrawals, promotional offers, and ways to contact the support team. After reading this review, you’ll be able to decide if you might want to sign up for Banger and why.
Games Catalog at Casino Banger
Banger boasts a rich and diverse game catalog that keeps continuously expanding. There are over a dozen game categories to choose from; you can switch between them in the left column of the main page. All the titles have an amazing design, soundtrack, and gameplay.

The casino buys games from around 40 established providers. To get to know their names, scroll down the left column on the main page. You’ll come across Belatra Games, BGaming, Ezugi, Mascot, NetEnt, and others. Tick the name of the preferred provider to filter its products.
Besides, there are four other filters to use. They’re located under the central ad banner, in the top right corner. They enable you to sort games by:
- Alphabetic order
- Reverse alphabetical order
- Novelty
- Popularity
Most games support the Demo mode. If you enable it, you won’t have to deposit cash into your account. You’ll be allowed to train with virtual coins that lack real-life value. In Demo mode, it’s impossible to win or lose a single BDT.
After you gain confidence, quit the Demo mode and click Play on the game’s icon. After that, you’ll be able to put real BDT at stake and withdraw your prize when you win.
Hundreds of Slots
The collection of slots is so large that you’ll be spoilt for choice. To explore it, you can click the More button at the end of the page, or just keep scrolling down and let the game icons upload automatically. To come back to the end of the list, click Scroll Up in the lower right corner.

The themes of slots are incredibly diverse: adventures, magic, treasure mining, celebrities, holidays, gems, animals, monsters, and many more. There are fruit machines in the catalog; they’re ideal for nostalgic people and players with little experience. Advanced players can indulge in slots with intricate bonus rounds and jackpots.
Over 70 Live Dealers
Live casino games are table games with live dealers. People love this game format for its interactive and visual aesthetics. Young and beautiful dealers broadcast in real time from nicely decorated rooms. You get the illusion of placing bets in a brick-and-mortar casino. You can send a message to the dealer and they can respond to it.

The selection of games includes blackjack, baccarat, poker, craps, monopoly, dreamcatcher and others. Most of them are available in several varieties that differ in their rules. The provider of these titles, Evolution, is one of the best brands in this niche on a global scale. The games will load fast and look awesome even on the small screen of a smartphone.
VSports Bets
To win money on the website of a conventional bookmaker, you need to be an expert in sports. You should follow the news about the selected discipline and watch matches to assess the performance of different teams. It takes a lot of time and effort.
Virtual sports were invented for people who want to have fun hassle-free. They imitate real-life sports, but in a make-believe universe. You enjoy the same adrenaline rush and you can place bets on the outcomes or other statistics of the events. It’s not necessary to have profound knowledge of any discipline.
The selection of virtual sports games at Banger Casino keeps growing. Their graphics are superb and the gameplay is fascinating. Even if you’ve never tried betting on sports before, it should be very easy for you to get started here.
Popular and Favorite Games
At the top of the left column on the main page, there are two buttons: Popular and Favorites.
If you click Popular, you’ll discover the items that others launch the most frequently. Apart from the high demand, these titles can have little in common. This selection might contain games of different genres, levels of difficulty and RTP. The contents of this page can change over time.
If you click Favorites, you’ll find yourself on an empty page. It’s up to you to add titles that you love the most there. To do so, open a game and click the star icon in the top-right corner. Thanks to the Favorites page, you’ll be able to come back with one click to the items that you’d like to launch again and again.
Crash Game Aviator
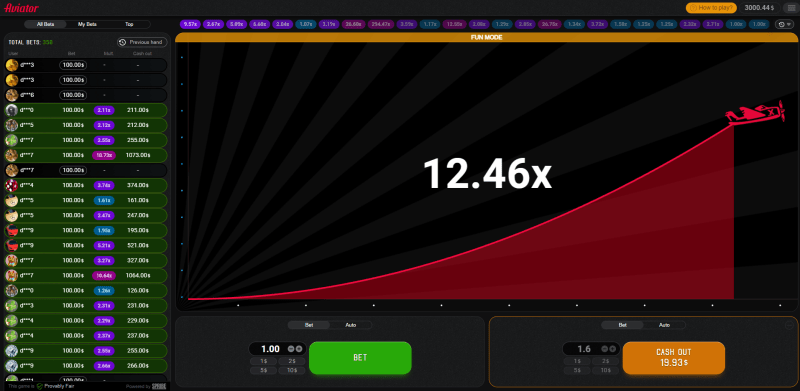
Aviator belongs to the innovative niche of crash games. A plane is taking off and your task is to cash out before it crashes. The mechanics of the game are extremely simple and resemble those of slots. The outcome depends on luck, but you may apply strategies to minimize your expenses. It’s a true gem that has revolutionized the online gambling industry.
Live Casino, Bangladesh-Style

Some titles in the Live Casino section are international. The rules of the games were invented in Europe and their dealers are Westerners. However, the Bangladeshi audience appreciates the chance to play games that are popular in Asia and interact with the dealers from the region. That’s why there are themed titles in the catalog: Dragon Tiger, Andar Bahar, Sic Bo, Bac Bo and others.
Bonuses, Tournaments and Special Offers
Bonuses and tournaments are essential for keeping customers happy and excited. Banger generously distributes special offers and organizes competitions. To find out about the opportunities, pay attention to banners and regularly visit the My Bonuses tab in your user profile. Plus, check the Tournaments section of the top horizontal menu of the main page.

There is a special balance for bonus funds in your wallet. Let’s have a look at how it functions, using an example of a promotional offer that requires a deposit:
- You deposit an amount of cash that is enough to activate the bonus.
- The bonus funds are credited to your bonus balance.
- You start wagering the offer, using cash from your real-money balance.
- After you run out of cash, you can keep on playing with the bonus funds.
You can transfer bonus funds to your real-money account, but only as much as the payout coefficient allows. This coefficient is indicated in the terms of the promotional offer. If it’s not specified, it equals one. To calculate the maximum sum that you can transfer, use this formula: multiply the amount of the bonus by the payout coefficient.
When wagering a bonus, keep in mind the different contributions of games:
| Table games, Poker, Video Poker, Baccarat, Blackjack, Roulette, Lotteries, Scratch Cards, Bingo, Keno, and Aviator | 0% |
| VSports, live games and TV games | 10% |
| Slots | 100% |
Some promotional offers enable you to request a withdrawal only after you’ve fully played through the bonus funds. Others let you withdraw ⅓ of what you have on your real-money balance if you have at least one active promotional offer.
A tournament is a competition focused on a specific game type. For instance, it can be treasure-themed slots or slots by a specific provider. To join a tournament, you should deposit cash and start playing the selected games. When you win, you’ll get a number of scores that are proportional to your winnings. There will be a leaderboard of the best-performing players.
A tournament can last a few days or a few weeks. Several people in the highest positions on the leaderboard will get their prizes. For instance, it can be cash, personalized bonuses, or new smartphones. Game providers often sponsor tournaments. It’s an excellent chance to make your gambling experience even more adrenaline-fueled.
Welcome Bonus for New Customers
Banger Casino Online has a lucrative welcome gift for new customers. Each individual can claim it only once, immediately after signing up for the platform. You’ll be able to get an increase on your initial deposit and free spins.
You’ll have 48 hours to wager the bonus funds with an x50 coefficient. This bonus is compatible only with slots. Before requesting a withdrawal, be ready to either play through all the bonus funds or cancel the bonus. If you fail to play through the funds within 48 hours, the bonus will be canceled automatically.
The maximum limit of this offer is 300 USD. If you win more, you won’t be able to withdraw the part of your prize that exceeds 300 USD.
Free spins will be credited to you in batches. For five consecutive days, you’ll be getting a package of 50 free spins. You’ll have 24 hours to wager on each batch.
ATTENTION: Some people think it’s too challenging to wager the welcome gift with an x50 coefficient within 48 hours. If you’re one of them, you can leave the offer deactivated. Remember that you won’t be allowed to come back to it later. Maybe it’s still worth trying because if you fail to wager the bonus on time, you’ll have a lot of fun anyway, and there will be no negative consequences.
How to Claim the Welcome Gift
To claim this gift, it’s enough to deposit small sums:
| How much do you deposit? | What you get |
| 5 USD | 100% increase in your deposit |
| 5 USD within one hour of the registration | 125% increase in your deposit |
| 15 USD | An increase in your deposit + 250 free spins |
In addition to making a deposit, you’ll need to claim the bonus in your user profile. The process is very straightforward: click the My Bonuses button in the left column of your profile, find the icon with the bonus and click Get.
ATTENTION: To be able to claim the welcome gift, make the deposit in a single transaction.
Loyalty Program Opportunities
The idea behind the loyalty program is simple and motivating. The more time and funds you spend at a gambling platform, the higher your level and the more privileges become available to you. You can get access to personalized bonuses, invitation-only tournaments, lower wagering coefficients and other perks. You might be among the first to try new games. Probably, a personal manager will be assigned to you.
Right now, the website of Banger Casino lacks information about the loyalty program. But it can appear at any moment. Meanwhile, you can check the list of bonuses that are available to you in your user profile. You’ll be likely to discover more and more offers there as you’ll be making progress at Banger.
How to Sign up for Banger
You can sign up for Banger Casino from your stationary computer or mobile device. The most important thing is to avoid creating multiple accounts. Regardless of which device you use, you should always log in with the same username and password.
Before you register, read the Terms and Conditions of Banger. To find them, scroll down the main page to the footer. Alternatively, you’ll discover the link to this document in the sign-up form. The text is a bit lengthy, but definitely worth your attention.
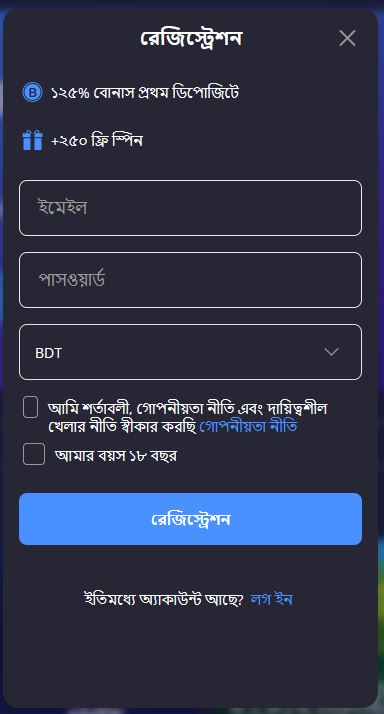
Here is the step-by-step guide to creating an account at Banger:
- Click the Sign Up button in the top right corner of the main page or any other casino page where it’s available.
- In a pop-up window in the center of the page, specify your password and email; the latter will serve as your username.
- Indicate your currency—BDT is the only option so far.
- Tick the box to confirm that you accept the Terms and Conditions of the platform.
- Tick the box to confirm that you’re 18 or older.
- Click Sign Up
Immediately after filling out the form, you can get down to placing bets.
ATTENTION: The rules of the platform prohibit creating multiple accounts per device, IP address, credit card and premise. It’s very easy to reveal duplicate accounts and close them. The administration will let you use your initial account, but there might be restrictions. For instance, you might lose access to selected bonuses.
How to Verify Your Identity
At the sign-up stage, you don’t need to reveal your detailed personal information. But it’s obligatory to share it to be allowed to withdraw funds. It’s a standard practice among all licensed casinos.
The administration will ask you for two papers:
- Passport—to prove that you have come of age
- Utility bill, issued no longer than 3 months ago—to prove that you live in a place where online gambling is allowed
Instead of your passport, you can show your ID or another similar document to managers. It needs to be government-issued and bear your name, photo and date of birth.
ATTENTION: Banger Casino will store your private data securely. You shouldn’t be afraid of leaks because it’s a licensed gambling platform that relies on advanced data protection technologies.
Typically, the verification takes a maximum of 72 hours. You just submit the documents and wait. However, each case is individual. The administration might ask you to provide additional papers or have a video call with them. Video calls might be necessary to make sure you share your own documents and not someone else’s.
If you refuse to verify your identity, you might not be able to keep on playing. The administration might suspend your account and cancel your active bets. Verification in a licensed casino doesn’t involve any risks, so you’d better complete it on time to enjoy gambling to the max.
Three Payment Systems at Your Disposal
To deposit and withdraw funds, you can use three payment systems: BKash, Nagad and Rocket. All of them are safe, popular and trustworthy. They support BDT. You’ll be able to deposit funds into your casino balance from the same wallet that you use for casual purchases. Plus, you won’t have to pay a conversion fee.
To check your current balance, you can take a look at any of these spots:
- Top right corner of the page
- Top part of the left column in your user profile
- The Top part of the popup window that you’ll use for deposits and withdrawals
The first two options will display both your real-money balance and your bonus one. In the popup window, you’ll see only the real-cash amount.
The limits for financial transactions are identical for all three systems:
| Minimum | Maximum | |
| Deposit | 400 BDT | 20,000 BDT |
| Withdrawal | 1,000 BDT | 20,000 BDT |
Please use only the wallets and accounts that bear your name. Otherwise, the casino might classify the transaction as suspicious and reverse it.
It’s better to use the same system for deposits and withdrawals. If you deposit funds through one system and withdraw them through another one, this might resemble money laundering. The casino administration might want to conduct an investigation.
ATTENTION: You should place bets only with the money that you obtained legally.
Easy Deposits
Without cash on your real-money balance, you won’t be able to launch any game in full-fledged play mode. Only Demo mode will be available to you. If you click Play, the pop-up window for depositing funds will open in the center of the page. You can also open it by clicking the wallet icon in the top-right corner of the page.
The Deposit tab in the popup window will be open by default. Choose a payment method. Type in the deposit amount manually or select one of the three options that the system offers: 400, 600 or 800 BDT. Click Continue. The casino will redirect you to the gateway of the chosen payment system. Deposits should be instant or almost instant.
ATTENTION: There are comprehensive video instructions for BKash and Nagad. Click the logo of one of these payment methods and then click the link under its logo in the next window. The instructions are less than one minute long.
Quick Withdrawals
To withdraw funds, open the same popup window and switch to the Withdraw tab. Select the system and manually type in the amount. The casino won’t suggest any amounts to you automatically. Type in your wallet number—or, if you use Nagad, your phone number. Click withdraw to finalize the transaction through the payment gateway.
The process is genuinely intuitive, so there are no video instructions. You can expect to receive cash in a maximum of 72 hours. First, the Banger managers will review and approve your application within 24 hours. Then, the payment system will need up to 48 hours to deliver the money to you.
Mobile Version of Banger Casino
The full functionality of Casino Banger is available on mobile devices. Just as on the desktop, you’ll be able to play games, deposit and withdraw cash, activate and wager bonuses, contact customer support and make use of the other features.
If you wish, you can open the Banger website in your smartphone’s browser. This casino is compatible with most modern browsers. Another way out is to download the Banger app.
Banger’s Android App
Some casinos place links to their mobile apps on their websites. Others don’t share the links; users need to contact customer support to ask for the link in private. Banger belongs to the second category. Don’t hesitate to ask for its app!
Banger’s iOS App
The situation with the iOS app is the same as with its Android counterpart. To get the download link, you should ask the support crew about it. Feel free to do it right in the live chat.
Biggest Benefits of Banger Casino
Now that you know the main facts about Banger Casino, let’s enumerate the key merits of this platform:
- License. It’s a safe and legal place to gamble.
- Modern design. The interface is eye candy.
- Intuitive layout. Even if you have never gambled before, you’ll quickly get used to this platform.
- Impressive game catalog There are over a dozen game categories to choose from, including hundreds of slots and around 70 live dealers.
- Asian-themed games, including live dealers. It’s a nice add-on for the Bangladeshi audience.
- Fast and secure financial transactions through BKash, Nagad and Rocket. You’ll be able to use BDT.
- Handy mobile version You’ll be able to gamble on an iPhone or an Android smartphone.
- Generous bonuses and tournaments. You can claim your first gift immediately after registration.
- Professional support. Their answers are prompt and helpful.
Honest Gameplay and Sensitive Data Protection
Casino Banger goes to great lengths to protect its customers’ sensitive data and ensure honest gameplay. Before you sign up, it would be wise to check the documents — the links to them are located in the footer:
- Terms and Conditions
- KYC & AML Policy
- Privacy and Security
- Responsible Gambling
Being a licensed platform, Banger meticulously fulfills international digital security standards. It allows independent audits that confirm its integrity.
Apart from the license, game providers also contribute to Banger’s bona fide. They equip their products with random number generators. It’s impossible to hack the algorithms of games or impact them in any other way. All the clients have equal odds of winning.
Professional Support
The support staff of Banger Casinos speaks fluent English and is always ready to solve any issues. The easiest way to get in touch with them is through live chat. To access it, you should sign up and sign in. There are two live chat buttons on the page:
- In the top right corner, close to the icon that leads to your user profile and the wallet icon
- In the left column of your user profile
It’s the fastest communication channel, perfect for urgent requests. It might take the operator only a few seconds to provide an answer to your question. The exact response time will depend on how many requests the support crew needs to handle simultaneously.
An alternative way is to send a message to [email protected]. When using the email, you might need to wait a bit longer than in the chat — but the staff will try to attend to you as promptly as they can. Plus, it will be easier for you to save the history of your conversations in your inbox. You might need it, for example, if you have questions about financial operations and attach documents to your messages.
The third method is submitting a question through a social network. Scroll down to the footer and you’ll see the links to Banger’s Instagram and Telegram.
Conclusion
Casino Banger in BD/Bangladesh operates with a Curacao license. It’s a legal gambling platform that accepts BDT. Anyone aged 18 or older can join it. You can sign up and play either on a stationary computer or a mobile device. The registration takes around one minute, and then, you’ll need to verify your identity with documents.
The catalog of games features hundreds of titles, including slots, live dealers, table games, crash games, virtual sports and others. Some titles with live dealers are Asian-themed and have Asian dealers. The themes and designs of many slots are Asia-inspired as well.
Banger welcomes new players with a bonus and treats its loyal customers with diverse promotional offers. To spice up the gameplay, you can take part in tournaments. You can deposit and withdraw funds through BKash, Nagad and Rocket. The helpful and professional support team will be glad to answer your questions at any moment.
To sum it up, if you live in Bangladesh and enjoy online gambling, you should try your luck at Banger Casino.
Frequently Asked Questions
Is It Safe to Place Cash Bets at Banger Casino in Bangladesh?
Banger Casino got its license in Curacao and legally caters to Bangladesh. It processes deposits and withdrawals through well-known and trustworthy payment systems: BKash, Nagad and Rocket. The platform keeps its customers’ private data fully confidential. You can trust this brand.
Which Security Measures Are Activated?
Banger was licensed in Curacao and complies with international gambling standards. It accepts international audits that guarantee the transparency of all casino processes. The platform buys games from world-famous providers that equip their products with random number generators. All new clients need to verify their identities with documents to prevent money laundering and other types of nefarious activities.
What Are the Best Games at Banger?
There is no one-size-fits-all answer to this question. The largest game category is slots; there are hundreds of them. The demand for them is always high. Live dealers are popular because they make the gaming experience interactive. Gamblers who’re looking for a change eagerly launch virtual sports and crash games, such as Aviator. At Banger, everyone can find something for their taste.
Are There Any Exclusive Titles?
So far, no titles are marked as exclusive in the catalog, but they can appear a bit later. Banger purchases games from around 40 well-known developers. Some of them might want to provide this casino with exclusive titles one day.
How to Send a Message to Customer Support?
The easiest way is to use live chat on the Banger website. To open it, sign up, sign in and click the chat button either in the top right corner of the page or in the left column of your user profile. Alternatively, you can submit your question to [email protected] or through a social network. The links to Banger’s Instagram and Telegram accounts are available in the footer of the website.
What’s the Average Response Time?
The response time might differ depending on how many requests the support crew has to handle. In the live chat, you might be able to receive an answer in a few seconds after submitting your question. If you prefer email or social networks, you might need to wait a bit longer.